主席の業務日誌・2010年09月28日
算数、解いてみた

2010年09月吉日
日本神国 国家主席府 主席官房総務企画課

9-28

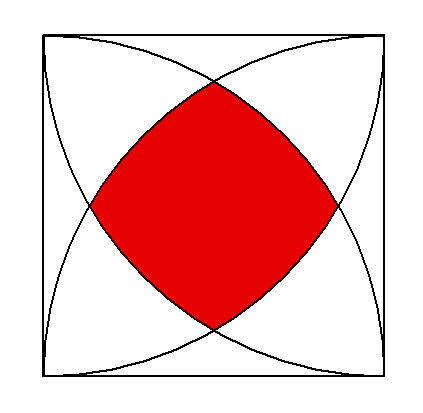
上記図の正方形の一辺は、a である。
このとき、赤い部分の面積を求めよ。
ただし、円周率は Π とする。


この問題、
http://vitzstar.blog51.fc2.com/blog-entry-2078.html
にて、発見した。
カンニング竹山が出ている番組を見ながら解いてみた。
なお、問題解答の過程で、竹山が貢献した部分は微塵もない。
（ただ、竹山は、そこそこ生き残って欲しい存在なので、これからもがんばっていただきたい物である。）


まず、赤い部分を直接計算することは難しい。
よって、定石どおり、正方形の面積から、周囲の余分な部分を抜いていく方向で対処する。



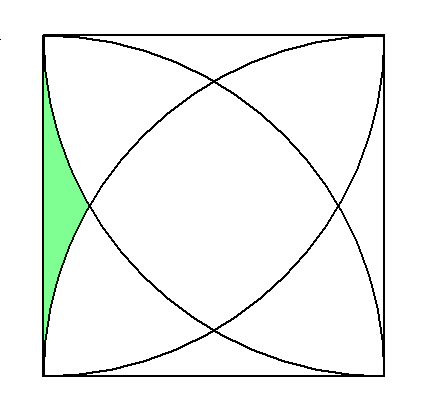
まず、緑の部分の面積を求める。
その為には、下記のように補助線を引く。



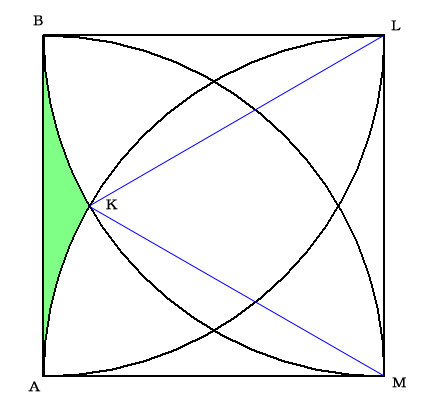
白い正方形から、正三角形ＫＬＭ・中心角30度の扇形ＢＫＬ・中心角30度の扇形ＡＫＭを、引き算する。
それぞれの面積の計算式は以下のとおり。

なお、ここから先の数式表記のルールは下記のとおりとなる。
a/b → ｂ分のａ
√c → ルートｃ
d^e → ｄのｅ乗

それでは本題に戻る。

正三角形ＫＬＭ ＝ 1/2 × a × a × sin 60 ＝ (√3)/4 a^2
扇形ＢＫＬ ＝ 扇形ＡＫＭ ＝ 30/360 × a × a × Π ＝ 1/12 Π a^2

よって、緑色の面積は、
正方形 − 正三角形ＫＬＭ − 扇形ＢＫＬ − 扇形ＡＫＭ
＝ a^2 − (√3)/4 a^2 − 1/12 Π a^2 − 1/12 Π a^2
＝ {1 - (√3)/4 - 1/6 Π} a^2

緑色の面積が分かったところで、次は、数の青色の場所。



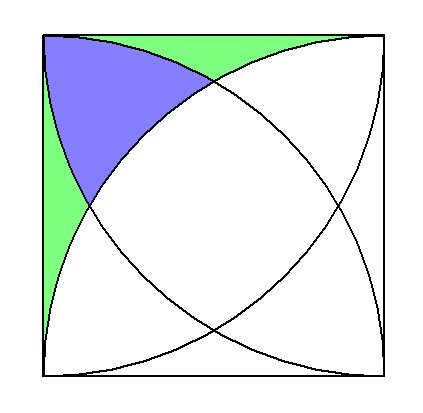
こちらは、正方形の面積から、中心角90度の半径 a の扇形の面積と緑色の部分の面積を引く。

よって、青色の面積は、
正方形 − 中心角90度の a の扇形の面積 − 緑色の部分
＝ a^2 − 90/360 × a × a × Π − 2 × {1 - (√3)/4 - 1/6 Π} a^2
＝ { -1 ＋ (√3)/2 ＋ 1/12 Π} a^2

ここまでくれば、解決したも同然。

最後に、赤い部分を求める。



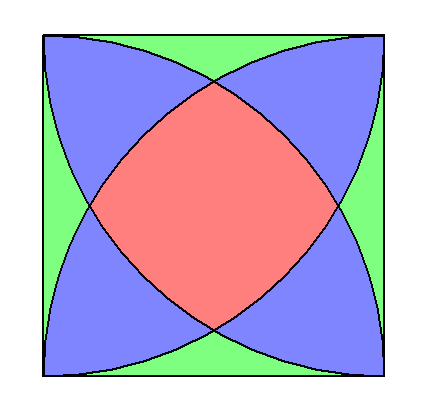
正方形全体の面積から、緑色の部分と青色の部分の面積を引き抜く。

よって、求める面積は、
赤色の面積 ＝ 全体の正方形の面積 − 緑色の面積 − 青色の面積
＝ a^2 − 4 × {1 - (√3)/4 - 1/6 Π} a^2 − 4 × { -1 ＋ (√3)/2 ＋ 1/12 Π} a^2
＝ a^2 − (√3) a^2 ＋ (1/3) Π a^2

以上で、求める面積が、
『 a^2 − (√3) a^2 ＋ (1/3) Π a^2 』
と、求められる。


……ちなみに、誰にも検算を頼んでいないので、間違っていても文句は言わないように。
解き方の流れだけでご勘弁を。

解いてる時間は短かったのだが、使った紙は、Ｂ５サイズ６枚以上。
まるで、サマーウォーズの小磯健二君並に、がりがりと、鉛筆転がして……、あ、あっちはボールペンか。


……
2010年9月29日、追記。
このページを作成後、問題提示者の kelog 氏が直々に検算してくださいました。
検算の結果、正解だそうです。
どうやら、中高生時代の算数の能力は衰えていなかった模様だ。
よかった。